{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "___\n",
    "\n",
    "<a href='http://www.pieriandata.com'><img src='../Pierian_Data_Logo.png'/></a>\n",
    "___\n",
    "<center><em>Copyright Pierian Data</em></center>\n",
    "<center><em>For more information, visit us at <a href='http://www.pieriandata.com'>www.pieriandata.com</a></em></center>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "collapsed": true
   },
   "source": [
    "# NumPy Operations"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Arithmetic\n",
    "\n",
    "You can easily perform *array with array* arithmetic, or *scalar with array* arithmetic. Let's see some examples:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])"
      ]
     },
     "execution_count": 1,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "import numpy as np\n",
    "arr = np.arange(0,10)\n",
    "arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])"
      ]
     },
     "execution_count": 2,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr + arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([ 0,  1,  4,  9, 16, 25, 36, 49, 64, 81])"
      ]
     },
     "execution_count": 3,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr * arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])"
      ]
     },
     "execution_count": 4,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr - arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "C:\\Anaconda3\\envs\\tsa_course\\lib\\site-packages\\ipykernel_launcher.py:3: RuntimeWarning: invalid value encountered in true_divide\n",
      "  This is separate from the ipykernel package so we can avoid doing imports until\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "array([nan,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.])"
      ]
     },
     "execution_count": 5,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# This will raise a Warning on division by zero, but not an error!\n",
    "# It just fills the spot with nan\n",
    "arr/arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "C:\\Anaconda3\\envs\\tsa_course\\lib\\site-packages\\ipykernel_launcher.py:2: RuntimeWarning: divide by zero encountered in true_divide\n",
      "  \n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "array([       inf, 1.        , 0.5       , 0.33333333, 0.25      ,\n",
       "       0.2       , 0.16666667, 0.14285714, 0.125     , 0.11111111])"
      ]
     },
     "execution_count": 6,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Also a warning (but not an error) relating to infinity\n",
    "1/arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([  0,   1,   8,  27,  64, 125, 216, 343, 512, 729], dtype=int32)"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr**3"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Universal Array Functions\n",
    "\n",
    "NumPy comes with many [universal array functions](http://docs.scipy.org/doc/numpy/reference/ufuncs.html), or <em>ufuncs</em>, which are essentially just mathematical operations that can be applied across the array.<br>Let's show some common ones:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,\n",
       "       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])"
      ]
     },
     "execution_count": 8,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Taking Square Roots\n",
    "np.sqrt(arr)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,\n",
       "       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,\n",
       "       2.98095799e+03, 8.10308393e+03])"
      ]
     },
     "execution_count": 9,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Calculating exponential (e^)\n",
    "np.exp(arr)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([ 0.        ,  0.84147098,  0.90929743,  0.14112001, -0.7568025 ,\n",
       "       -0.95892427, -0.2794155 ,  0.6569866 ,  0.98935825,  0.41211849])"
      ]
     },
     "execution_count": 10,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Trigonometric Functions like sine\n",
    "np.sin(arr)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 11,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "C:\\Anaconda3\\envs\\tsa_course\\lib\\site-packages\\ipykernel_launcher.py:2: RuntimeWarning: divide by zero encountered in log\n",
      "  \n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "array([      -inf, 0.        , 0.69314718, 1.09861229, 1.38629436,\n",
       "       1.60943791, 1.79175947, 1.94591015, 2.07944154, 2.19722458])"
      ]
     },
     "execution_count": 11,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# Taking the Natural Logarithm\n",
    "np.log(arr)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Summary Statistics on Arrays\n",
    "\n",
    "NumPy also offers common summary statistics like <em>sum</em>, <em>mean</em> and <em>max</em>. You would call these as methods on an array."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])"
      ]
     },
     "execution_count": 12,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr = np.arange(0,10)\n",
    "arr"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "45"
      ]
     },
     "execution_count": 13,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr.sum()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 14,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "4.5"
      ]
     },
     "execution_count": 14,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr.mean()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 15,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "9"
      ]
     },
     "execution_count": 15,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr.max()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<strong>Other summary statistics include:</strong>\n",
    "<pre>\n",
    "arr.min() returns 0                   minimum\n",
    "arr.var() returns 8.25                variance\n",
    "arr.std() returns 2.8722813232690143  standard deviation\n",
    "</pre>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Axis Logic\n",
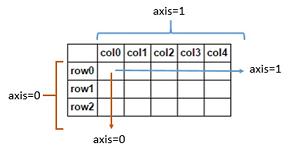
    "When working with 2-dimensional arrays (matrices) we have to consider rows and columns. This becomes very important when we get to the section on pandas. In array terms, axis 0 (zero) is the vertical axis (rows), and axis 1 is the horizonal axis (columns). These values (0,1) correspond to the order in which <tt>arr.shape</tt> values are returned.\n",
    "\n",
    "Let's see how this affects our summary statistic calculations from above."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 16,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([[ 1,  2,  3,  4],\n",
       "       [ 5,  6,  7,  8],\n",
       "       [ 9, 10, 11, 12]])"
      ]
     },
     "execution_count": 16,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr_2d = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])\n",
    "arr_2d"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 17,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([15, 18, 21, 24])"
      ]
     },
     "execution_count": 17,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr_2d.sum(axis=0)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "By passing in <tt>axis=0</tt>, we're returning an array of sums along the vertical axis, essentially <tt>[(1+5+9), (2+6+10), (3+7+11), (4+8+12)]</tt>\n",
    "\n",
    "<img src='axis_logic.png' width=400/>"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 18,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "(3, 4)"
      ]
     },
     "execution_count": 18,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "arr_2d.shape"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "This tells us that <tt>arr_2d</tt> has 3 rows and 4 columns.\n",
    "\n",
    "In <tt>arr_2d.sum(axis=0)</tt> above, the first element in each row was summed, then the second element, and so forth.\n",
    "\n",
    "So what should <tt>arr_2d.sum(axis=1)</tt> return?"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "collapsed": true
   },
   "outputs": [],
   "source": [
    "# THINK ABOUT WHAT THIS WILL RETURN BEFORE RUNNING THE CELL!\n",
    "arr_2d.sum(axis=1)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Great Job!\n",
    "\n",
    "That's all we need to know for now!"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.6.6"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 1
}