29 KiB
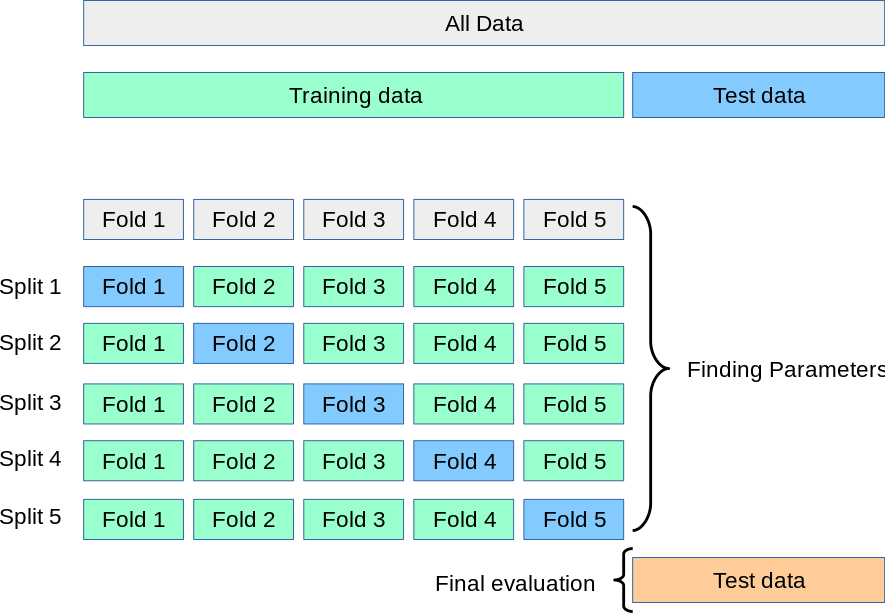
Introduction to Cross Validation¶
In this lecture series we will do a much deeper dive into various methods of cross-validation. As well as a discussion on the general philosphy behind cross validation. A nice official documentation guide can be found here: https://scikit-learn.org/stable/modules/cross_validation.html
Imports¶
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
Data Example¶
df = pd.read_csv("../DATA/Advertising.csv")
df.head()
Train | Test Split Procedure¶
- Clean and adjust data as necessary for X and y
- Split Data in Train/Test for both X and y
- Fit/Train Scaler on Training X Data
- Scale X Test Data
- Create Model
- Fit/Train Model on X Train Data
- Evaluate Model on X Test Data (by creating predictions and comparing to Y_test)
- Adjust Parameters as Necessary and repeat steps 5 and 6
## CREATE X and y
X = df.drop('sales',axis=1)
y = df['sales']
# TRAIN TEST SPLIT
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# SCALE DATA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
Create Model
from sklearn.linear_model import Ridge
# Poor Alpha Choice on purpose!
model = Ridge(alpha=100)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
Evaluation
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_pred)
Adjust Parameters and Re-evaluate
model = Ridge(alpha=1)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
Another Evaluation
mean_squared_error(y_test,y_pred)
Much better! We could repeat this until satisfied with performance metrics. (We previously showed RidgeCV can do this for us, but the purpose of this lecture is to generalize the CV process for any model).
Train | Validation | Test Split Procedure¶
This is often also called a "hold-out" set, since you should not adjust parameters based on the final test set, but instead use it only for reporting final expected performance.
- Clean and adjust data as necessary for X and y
- Split Data in Train/Validation/Test for both X and y
- Fit/Train Scaler on Training X Data
- Scale X Eval Data
- Create Model
- Fit/Train Model on X Train Data
- Evaluate Model on X Evaluation Data (by creating predictions and comparing to Y_eval)
- Adjust Parameters as Necessary and repeat steps 5 and 6
- Get final metrics on Test set (not allowed to go back and adjust after this!)
## CREATE X and y
X = df.drop('sales',axis=1)
y = df['sales']
######################################################################
#### SPLIT TWICE! Here we create TRAIN | VALIDATION | TEST #########
####################################################################
from sklearn.model_selection import train_test_split
# 70% of data is training data, set aside other 30%
X_train, X_OTHER, y_train, y_OTHER = train_test_split(X, y, test_size=0.3, random_state=101)
# Remaining 30% is split into evaluation and test sets
# Each is 15% of the original data size
X_eval, X_test, y_eval, y_test = train_test_split(X_OTHER, y_OTHER, test_size=0.5, random_state=101)
# SCALE DATA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_eval = scaler.transform(X_eval)
X_test = scaler.transform(X_test)
Create Model
from sklearn.linear_model import Ridge
# Poor Alpha Choice on purpose!
model = Ridge(alpha=100)
model.fit(X_train,y_train)
y_eval_pred = model.predict(X_eval)
Evaluation
from sklearn.metrics import mean_squared_error
mean_squared_error(y_eval,y_eval_pred)
Adjust Parameters and Re-evaluate
model = Ridge(alpha=1)
model.fit(X_train,y_train)
y_eval_pred = model.predict(X_eval)
Another Evaluation
mean_squared_error(y_eval,y_eval_pred)
Final Evaluation (Can no longer edit parameters after this!)
y_final_test_pred = model.predict(X_test)
mean_squared_error(y_test,y_final_test_pred)
## CREATE X and y
X = df.drop('sales',axis=1)
y = df['sales']
# TRAIN TEST SPLIT
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# SCALE DATA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
model = Ridge(alpha=100)
from sklearn.model_selection import cross_val_score
# SCORING OPTIONS:
# https://scikit-learn.org/stable/modules/model_evaluation.html
scores = cross_val_score(model,X_train,y_train,
scoring='neg_mean_squared_error',cv=5)
scores
# Average of the MSE scores (we set back to positive)
abs(scores.mean())
Adjust model based on metrics
model = Ridge(alpha=1)
# SCORING OPTIONS:
# https://scikit-learn.org/stable/modules/model_evaluation.html
scores = cross_val_score(model,X_train,y_train,
scoring='neg_mean_squared_error',cv=5)
# Average of the MSE scores (we set back to positive)
abs(scores.mean())
Final Evaluation (Can no longer edit parameters after this!)
# Need to fit the model first!
model.fit(X_train,y_train)
y_final_test_pred = model.predict(X_test)
mean_squared_error(y_test,y_final_test_pred)
Cross Validation with cross_validate¶
The cross_validate function differs from cross_val_score in two ways:
It allows specifying multiple metrics for evaluation.
It returns a dict containing fit-times, score-times (and optionally training scores as well as fitted estimators) in addition to the test score.
For single metric evaluation, where the scoring parameter is a string, callable or None, the keys will be:
- ['test_score', 'fit_time', 'score_time']
And for multiple metric evaluation, the return value is a dict with the following keys:
['test_<scorer1_name>', 'test_<scorer2_name>', 'test_<scorer...>', 'fit_time', 'score_time']
return_train_score is set to False by default to save computation time. To evaluate the scores on the training set as well you need to be set to True.
## CREATE X and y
X = df.drop('sales',axis=1)
y = df['sales']
# TRAIN TEST SPLIT
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# SCALE DATA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
model = Ridge(alpha=100)
from sklearn.model_selection import cross_validate
# SCORING OPTIONS:
# https://scikit-learn.org/stable/modules/model_evaluation.html
scores = cross_validate(model,X_train,y_train,
scoring=['neg_mean_absolute_error','neg_mean_squared_error','max_error'],cv=5)
scores
pd.DataFrame(scores)
pd.DataFrame(scores).mean()
Adjust model based on metrics
model = Ridge(alpha=1)
# SCORING OPTIONS:
# https://scikit-learn.org/stable/modules/model_evaluation.html
scores = cross_validate(model,X_train,y_train,
scoring=['neg_mean_absolute_error','neg_mean_squared_error','max_error'],cv=5)
pd.DataFrame(scores).mean()
Final Evaluation (Can no longer edit parameters after this!)
# Need to fit the model first!
model.fit(X_train,y_train)
y_final_test_pred = model.predict(X_test)
mean_squared_error(y_test,y_final_test_pred)